2016年新高考1卷和浙江卷的分值比例分析

这篇文章跟我之前写过的一个回答内容大致相似，后续有时间的话也会分享下本人对其他地区高考数学试卷的一些看法~

本文没有具体的解题方法，讲的是一些做题思路、检查方法和备考方向之类的。对于平时成绩能在130、140的同学来说，食用效果更佳~

整体评价

总体来看，今年的新高考1卷确实是非常难，准确的说是比较恶心。在我看来，这张试卷除了18题和20题出得有点新意，其他题目应该都是大家平时联考中有所接触的题型。这张试卷其实更像一张高三联考的试卷，没有特别难的压轴题2016年新高考1卷和浙江卷的分值比例分析，但从头到脚做起来都非常麻烦，从选择题第3题开始就没有省油的灯了，易中难题型的分值比例大致为2：7：1。对于平时联考能取得较高分数的同学来说，这张试卷应该也能得到一个不错的成绩。

跟浙江卷对比：新高考1卷和浙江卷难度都很大，但是在两个维度上的难。浙江卷的考试题只有送分题和送命题两种题型，选择压轴题技巧性非常强，偏向竞赛或自主招生强基计划的考试题；大题最后两道都是欧皇难度，圆锥曲线技巧性太强，导数证明又太过麻烦。

跟全国卷1对比：全国卷1更像一张高考试卷，不同难度题目的分值比例大致为6：2：2。全国卷1最后两道大题其实都比新高考1卷更难，尤其是导数压轴题，过程非常繁琐，要拿满分是相当困难的；圆锥曲线证明过定点问题思路也不是很清晰，因为这道题包装得过于吓人了......因此理论上来讲，在不考虑考试时间限制的情况下，全国卷1拿满分的难度更大一些；新高考1卷拿不到高分大多是因为计算量过大，后面时间不足而做不完。

逐题解析

1~3：定量计算非定性分析的选择题嘛数学拆补法，你算出的答案符合某个选项基本就是对的数学拆补法，没啥好检查的

4：这题考察的是棱台体积公式。记住了这个公式就很简单，没记住就只有靠蒙或现场推导公式了。这里我想说的是，咱们在一轮复习或是平时学习的时候，对于这些数学公式和定理一定要理解，最好能自己推导一遍。比如这里，棱台体积公式其实可以补全成两个棱锥，利用棱锥体积公式和相似性质把它推导出来。希望大家要明白一点：公式推导本质上也是一道题，而且比那些所谓的模拟卷的质量要高很多！今年高考题明显就是反套路化，更侧重于考察学生的数学思维而不是做题能力，而推导公式有助于提高大家的数学思维。

棱台的体积公式是 V=\frac{1}{3}(S+S'+\sqrt{SS'})h ，如何去理解以至记住这个公式呢，或者说你想起了棱台公式，怎么检验自己记住的公式对不对呢。可以试着这样去理解：棱台本身就是介于棱锥和棱柱之间的，所以棱台体积公式一定也是介于棱锥和棱柱体积公式之间。当 S’=0 时数学拆补法，就是棱锥，此时棱台的体积公式应该能转为棱锥的体积公式 V=\frac{1}{3}Sh ；当 S=S' 时，就转换成棱柱的体积公式 V=Sh 。如果满足这两个极限取值，就说明你这个公式没有记错。这种思维也可以用于考试时检查答案是否正确，比如后面的第11题！

5：考察互质的概念，穷举法即可

6：算出 \omega 之后代入函数看看是否满足关于 (\frac{3}{2}\pi,2) 点对称

7：这道题应该放在第8题的位置比较合适，放在这里确实有点难为考生了。我个人不建议高中去泰勒展开等高深的高数知识，只要了解它的思路，用高中的方法去构造函数也能很快做出来。比如这道题，一看就是很常规的函数构造题。我们不妨设 x=0.1 ，那么 a, b ,c 可以用 x 以一种最恰当的形式表示出来。很直观的可以看出 a=xe^{x} ，根据做题经验也可以得到 c=-ln(1-x) ；然后最难的就是 b 该怎么表示，当然这里可以表示成 b=\frac{x}{1-x} 。注意，这里的构造不是一蹴而就的，是咱们多次尝试构造试出来的！

8：这题如果侧棱长的取值范围是 3\leq l \leq 3\sqrt{2} ，那么可以只求 l=3和l=3\sqrt{2} 两个极端情况，分别代表体积的最小值和最大值，因为这种情况正四棱锥只在一个半球内，底面积和高是同时增大的，所以体积是单调递增的。但是 3\sqrt{2}\leq l \leq 3\sqrt{3} 时，如果 l 增大，那高也在增大，而底面积却在减小，无法判断棱锥体积的单调性，因此才要写出体积函数的表达式再求导考虑单调性！所以这道题不是一上来就无脑求导的，这里面也很多技巧可用。

9：建系法最快，但我还是教学生要用纯几何法去做，平时得注意培养下空间思维。这题限定了是正方体，因此设完边长为1后，所有线段的长度都可以准确求出来。这样的话就涉及到一个模型：已知边长求夹角，解决方法就是余弦定理。在任何一个三角形中，已知三边边长都可以准确求出角度2016年新高考1卷和浙江卷的分值比例分析，这道题也同理可做。

10：很常规的一道题，C选项考察的是三次函数的对称中心。这道题没有二次项，考得稍微容易一点。对于一个含二次项的三次函数 f(x)=ax^{3}+bx^{2}+cx+d 来说，它的对称中心是哪个点，以及怎么去证明推导，这是大家在做完试卷后需要拓展的知识。建议大家不要去记二级结论，关键在于怎么去推导证明这些二级结论，高考并考察的是咱们的思维和能力，并不是单纯考察几个结论或性质。

11：关于C和D选项，需要大量的计算才能证出来。怎么去检验你最终算的关于直线斜率 k 的表达式是否正确呢，用第4题的极限思维去解。注意到当斜率 k=2 时直线与抛物线相切，即点P、Q重合为点A。对于C选项 |OA|^{2}">|OP|\cdot|OQ|>|OA|^{2} ，如果你算出的 \left| OP\right|\cdot|OQ| 的表达式在 k=2 时的取值恰好为 |OA|^{2} ，则说明计算没问题。否则就意味出现了计算错误，需要返回重新计算。

14：如果这道题要你求出所有的公切线，咱就先设直线方程 l:y=kx+m ，就有斜率和截距两个待求参数。

注意注意注意！！！

这里有个方程思想：一个未知数一个方程，两个未知数两个方程，n个未知数n个方程。这个思维对于大家解题非常实用，可以用来判断自己列出的方程组是否可解、是否还有隐藏条件没用到。这里两个未知数，只需要两个方程，与两个圆相切分别各列一个方程，所以就能解出斜率和截距了。

15：比较常规，不多讲

17：求出通项公式后代入条件检查是否满足题目条件，然后注意 n=1,2 时有没有特殊取值，这里极容易出错。然后第（2）问如果你能证出恰好小于2，那就保证能拿下这10分了。

18：第（1）问也是代入判断是否满足条件，第（2）问不难，但是真的恶心，算出的答案也巨离谱，很理解考场上的同学做这道题是啥感受。出题老师我跪您一个吧......

19：第（2）问求二面角 A-BD-C 的正弦值，可以用纯几何法来验证结果。思路为：过点C作BD的垂线，垂足为点E。由于 \Delta ABD和\Delta ACD 具有对称性，所以AE也是BD的垂线，从而 \angle AEC 就是二面角 A-BD-C ，接下来就是用余弦定理求出 \angle AEC 的余弦值，再算出正弦值。建议有能力的同学还是学好纯几何法，建系法做题、纯几何检查，可以保证100%拿下这道送分题。

20：这道题我认为出得很有新意，但其实没啥必要。第（1）问证明题更像是大学里概率论里的题型，这张试卷的这种考法一定是高中概率题的先例。看得出来最近几年越来越注重考察概率统计了，圆锥曲线和导数题越是些老生常谈的题型，反而这种概率题需要大家注重复习。

21：

2022年新高考1卷数学第21题

第（1）问有两种解法：第一种是设 直线PQ：y=kx+m ，然后根据 AP和AQ 的斜率之和为0求出 k和m 的关系式；第二种是设直线 AP 的斜率为k，从而直线 AQ 的斜率为-k，然后直接计算 PQ 的斜率。咱们处理问题时有一个原则：未知数能少设尽量少设。所以第二种做法才是这道题最简单的方法。

检查点：

曲线方程检查：算完 a^{2}=2 之后，将 A(2,1) 代入看是否满足曲线方程方程联立检查：设直线 AP：y=k(x-2)+1 与双曲线方程 \frac{x^{2}}{2}-y^{2}=1 联立，可得关于 x 的方程：

(2k^{2}-1)x^{2}+(4k-8k^{2})x+8k^{2}-8k+4=0

从而由韦达定理可得：

x_{1}+x_{2}=\frac{8k^{2}-4k}{2k^{2}-1}

x_{1}\cdot x_{2} = \frac{8k^{2}-8k+4}{2k^{2}-1}

重点来了！！！

重点来了！！！

重点来了！！！

由于其中一个解是 A 点的横坐标 x_{A}=2 ，可以用韦达定理的两个式子分别求出 x_{P} 的值。如果这两个式子求出的 x_{P} 的值是相同的，恭喜你，你的计算过程没有出现问题！

Tips：

之后对于直线 AQ 与双曲线的联立，其实可以利用换元法的思想，将 AP 与双曲线联立的方程中的 k 项用 -k 来代替，避免重复计算：

(2(-k)^{2}-1)x^{2}+(4(-k)-8(-k)^{2})x+8(-k)^{2}-8(-k)+4=0

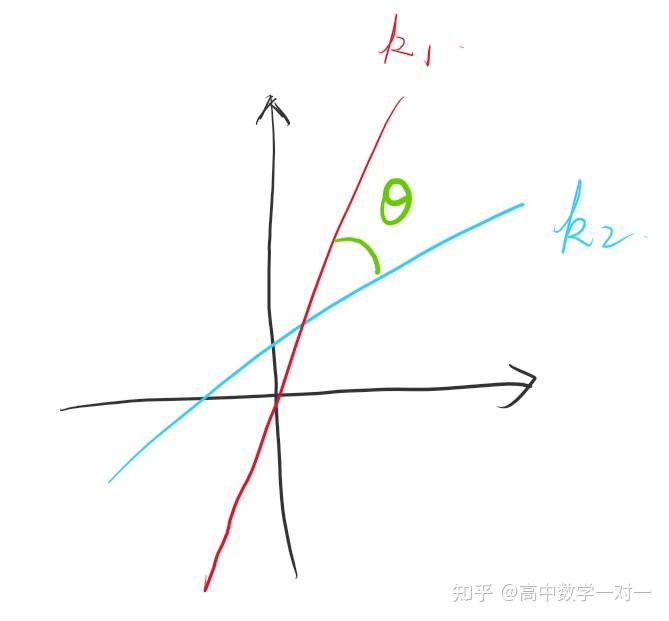
第（2）问大家可能没接触过这种题型，但其实思路很清晰，用一个半角公式求出 AP 斜率再无脑计算就行了。我再补充一个类似的情形：直角坐标系里已知两条直线的斜率，求夹角大小。这可以用两角和差公式去求：

tan\theta=\frac{k_{1}-k_{2}}{1+k_{1}k_{2}}

22：很常规的同构函数题吧，知道了就会证，没啥好说的。

文末

一张试卷拿满分，绝不是只会几种方法那么容易，需要数学思维和答题技巧来辅助我们算的更快更准！有些思维确实是老师教不到的，需要咱们多去思考，或多跟同学交流探讨~

希望这些建议可以帮助到大家，后续有时间我再分享下自己对其他地区高考卷的一些看法和思路吧~

• 上一篇： 浅谈一下全国一卷数学此处浅谈
• 下一篇：奇门遁甲的四层框架思维思维体系及其应用策略分析